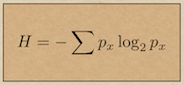How Information content is calculated from uncertainty
Twenty QuestionsThe basic idea of information is easy to get.
A lot of people explain information through the parlour game "20 questions". The idea is to guess what object a person is thinking of by asking a series of up to 20 questions with strictly only yes / no answers. The point of this is that each answer (being strictly binary) gives exactly 1 bit of information. When the questioner guesses correctly after n≤20 questions, they will have received n bits of information.
Of course that is rather artificial and limited.
-------------
Here we explain, with an illustration, how information can be quantified in way that is a little more flexible.
What follows is an explanation based on a short story, found in Zernike (1972) [see our library page] and a little updated.
Here goes...
You friend sends you a text message saying that at some point next week she will visit you: it could be any day of the week and any time (on the hour) between 9am and 5pm. So you have 7 x 9 = 63 possible hours when she could arrive. The end of the text says that she will confirm the day and time in later messages. Next day, you receive another text saying ‘Wednesday’. The number of possibilities has now shrunk to just 9. Later in the afternoon you hear from her again: this time another terse message saying ‘11am’. By this point you know exactly when she will appear because the number of possible hours of arrival is now only 1. So the first received information ( call it I1) gave you 63 possibilities (a range of uncertainty), the second (I2) got that down to 9 and the third (I3) left you with no uncertainty: just one possibility. Claude Shannon defined ‘information’ as a decrease in the uncertainty of a receiver, which exactly fits this little story. We can quantify the amount of information in the second and third text messages, using the change in uncertainty, noting that each text added to the information we had, to reduce your uncertainty. The total information received gave you no doubt about the time of arrival, so zero uncertainty. Intuitively, we would add the information in each text to get to this (it is, after all the total information (IT) that reduced the uncertainty to zero) IT = I1 + I2 + I3. However, uncertainty is a measure of the number of possibilities, that is it works with probability and probabilities combine by multiplying (e.g. the chance of throwing two sixes in a row is 6x6=36). Another way to put it is that just after the second text, the probability that it will be a particular hour on Wednesday (from 9am to 5pm) rises from 1/63 to 1/9, multiplying by 7, because the probability of Wednesday rises from 1/7 to 1 after the second text. Now, let me ask, what is it that has the effect of multiplying when it is added? The answer is logs, So, adding the log of probabilities has the effect of multiplying them (which is what we need). For this reason, Shannon deduced that the information content of a message was the log of the change in probabilities that it caused. So, we have that intuitively the total information of the texts is I1 + I2 + I3 = IT. And this is quantified by adding the probabilities of arrival hour:
P1 after the first text; P2 after the second and P3 after the third. Using logs in base 2 (we'll explain in a moment):
for the second two messages
I2 = K (log2 P1 - log2 P2) = K (-5.98 - -3.17)
I3 = K (log2 P2 - log2 P3) = K (-3.17 - 0) (note P3 is 1, so its log is zero).
We used base 2 for the logs, because this naturally gives units in binary bits of information.
Recall that a binary bit [1or 0] is the smallest possible difference and therefore smallest possible unit of data and by implication, of information. There are just two possibilities in a single bit, with probability of each being 0.5 and you don’t know which it will be until you ‘receive’ the bit of information, so the bit changes your uncertainty by K (log2 0.5 - log2 1) = K( -1 - 0) = K. Now it is sensible, since this is the smallest unit of information, to define it equal to 1 bit. Thus K has the (convenient) value of -1 exactly, if we use log in base 2.
We can now work out the information content of the second two text messages:
I2 = 2.8 bits and I3 = 3.2 bits (roughly) and the total information of both messages was about 6 bits. Indeed if your friend had told you Wednesday at 11am in the second message, then that would have been worth about 6 bits and -( log2 1/63 - log2 1) is indeed about 6.
At this point it is important to notice that we are dealing with the semantic information content of the messages, not their syntactic information content (which ignores their meaning and just considers the probability of a sequence of letters).
One last thing, the first text message said that your friend would come sometime next week and we have not yet accounted for that information. This is because it is a bit difficult to specify: on the strict interpretation of the evidence and nothing but the evidence provided, you had no idea at all when, or even whether she would arrive, so the uncertainty was technically infinite. This is where the numerical calculations rather break down - they only work with finite possibilities. It would be easy to work out if you knew she would be coming sometime this year.